PROPIEDADES DE LAS PROPORCIONES
Las principales propiedades que se cumplen en toda proporción a/p = b/q son:
- El producto de los extremos es igual al producto de medios a*q = b*p
- Si se invierten los términos se obtiene otra proporción p/a = q/b
- Si se intercambian los extremos o medios se obtienen otra proporción q/p = b/a
- Si se suma o se resta uno en ambos miembros de la igualdad se obtiene otra proporción (a + p) /p = (b +q) /q o también (a - p) /p = (b - q) /q
EJEMPLO: Determinar si las siguientes razones son proporciones.

* Determinamos si es proporción utilizando alguna de las propiedades anteriores.
Si multiplicamos los extremos debe de ser igual a la multiplicación de los medios 12 x 16 =192; 32 x 6 = 192; por lo tanto si es una proporción.

* Determinamos si es proporción utilizando alguna de las propiedades anteriores.
5 x 0,75 = 3,75; 7 x 0,25 = 1,75; por lo tanto no es una proporción ya que los dos resultados no son iguales.

Si multiplicamos los extremos debe ser igual a la multiplicación de los medios.
6 x 3 = 18; 4 x 8 = 32; por lo tanto no es una proporción.
EJEMPLO: Encontrar el término desconocido en cada proporción.

* Despejamos la variables n.

Despejamos la variable b y simplificamos.
EJEMPLO: Determinar el valor del lado desconocido, si las medidas de los lados correspondientes de los dos triángulos son proporcionales
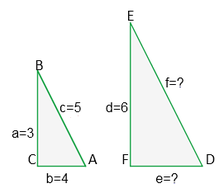
1- Primero se determina si las medidas de los 2 triángulos son proporcionales. Como si son se cumple que a/b = d/e.

2- Aplicamos la primera propiedad y despejamos la variable e.

3- Planteamos otra proporción. Reemplazamos el valor de e y despejamos la variable f.
El siguiente video te podrá aclarar un poco más sobre los términos razón y proporción
En la siguiente página podrás poner a prueba lo aprendido, realiza los ejercicios propuestos y luego observa la solución.
http://odas.educarchile.cl/objetos_digitales/odas_matematicas/17/index.html
 Hay una fuerza motriz
más poderosa que el
vapor, la electricidad y
la energía atómica: la voluntad.
Hay una fuerza motriz
más poderosa que el
vapor, la electricidad y
la energía atómica: la voluntad.