POLÍGONOS SEMEJANTES

Dos figuras son semejantes cuando tienen la misma forma, aunque tengan diferente tamaño. Por ejemplo una copia ampliada es semejante al objeto fotocopiado.

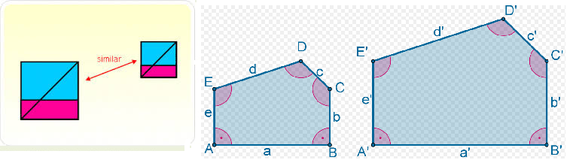
Se puede observar que dos polígonos son semejantes si hay una correspondencia entre los vértices de tal manera que:

  • Los ángulos correspondientes son congruentes.
  • Los lados correspondientes son proporcionales.

EJEMPLO: Determinar si los siguientes polígonos son semejantes, teniendo en cuenta que el cuadrado mide 3 cm de lado y el rectángulo mide 3 cm de ancho y 6 cm de largo.

 

Verificamos que se cumplan las condiciones anteriores:

 

  • Como las figuras son un cuadrado y un rectángulo, sus ángulos internos miden 90º, con lo cual se cumple la primera condición.

 

  • Debemos establecer relaciones entre los 2 cuadriláteros. Como las razones no son iguales, los lados no son proporcionales, por lo tanto las figuras no son semejantes.

EJEMPLO: Determinar si los siguientes polígonos son o no semejantes.

  1. Las dos figuras tienen el mismo ángulo, es decir, que son congruentes de 31°, por lo tanto cumple con la primera condición.
  2. Ahora los lados no son proporcionales, por lo tanto no cumple con la segunda condición.

Como cumple solo una condición por lo tanto las dos figuras no son semejantes. 

EJEMPLO: Determinar si las siguientes figuras son o no semejantes.

 

 

 

 

EJEMPLO: En un mapa a escala 1 : 50.000, la distancia entre dos pueblos  P y Q, es 11 cm. ¿Cuál es la distancia real expresada en kilómetros entre P y Q?

 

 

EJEMPLO: En un mapa a escala 1 : 50.000, la distancia real entre dos pueblos  M y N, es 18 Km. ¿Cuál es la distancia a la que se encuentran en el mapa?

  • Lo primero es que debemos de convertir los 18 km a cm, y lo que realizamos multiplicando 18 x 100.000 = 1.800.000

En los siguientes enlaces podrás obtener más información acerca de los polígonos semejantes, además podrás practicar lo aprendido.

https://www.edu.xunta.es/espazoAbalar/sites/espazoAbalar/files/datos/1491480036/contido/ud9_teorema_Thales_y_semejanza/21_figuras_semejantes.html

https://www.ck12.org/book/CK-12-Geometra-Edicin-Espaola/section/7.3/

https://compartirpalabramaestra.org/documentos/compartirsaberes/g-estudiantes_congruencia-y-semejanza.pdf