Hay una fuerza motriz
más poderosa que el
vapor, la electricidad y
la energía atómica: la voluntad.
CRITERIOS DE SEMEJANZA
Para comprobar que dos triángulos son semejantes no es necesario comprobar siempre que los tres ángulos sean congruentes y que los tres lados sean proporcionales, existen algunos criterios que permiten comprobar la semejanza con menos condiciones.
CRITERIO LADO - LADO - LADO (L-L-L)
Dos triángulos son semejantes si sus lados correspondientes son proporcionales.
Si se comprueba que los lados correspondientes de dos triángulos son proporcionales, no hay necesidad de comprobar que los ángulos son congruentes.
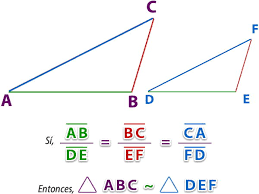
EJEMPLO: Determinar si los siguientes triángulos son semejantes entre sí.
- Como las razones son iguales, los lados de ambos triángulos son proporcionales y en consecuencia se tiene que el triángulo ABC es semejante al triángulo DEF.
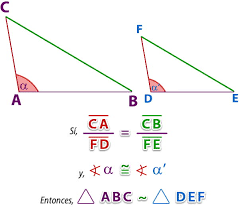
CRITERIO LADO - ANGULO - LADO (L-A-L)
Dos triángulo son semejantes si dos pares de lados correspondientes son proporcionales y los ángulos comprendidos entre ellos son congruentes.
Para comprobar que el triángulo ABC es semejante con el triángulo DEF, basta con verificar que el lado AB y AC son proporcionales con DE y DF, respectivamente y que el ángulo A es congruente con el ángulo D.
EJEMPLO: Determinar si los siguientes triángulos son semejantes entre sí.
- Como los lados son proporcionales y el ángulo D es igual al ángulo A, por lo tanto los dos triángulos son semejantes.
CRITERIO ÁNGULO - ANGULO (A-A)
Dos triángulos son semejantes si dos ángulos correspondientes son congruentes.
Para comprobar que el triángulo ABC es semejante con el triángulo DEF, sólo basta con comprobar que el ángulo A y el ángulo D son congruentes con el ángulo C y el ángulo F respectivamente.
EJEMPLO: Determinar si los siguientes triángulos son semejantes entre sí.
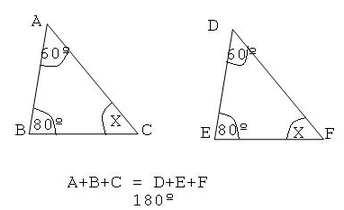
- En este caso no hay necesidad de comprobar que el ángulo C es congruente con el ángulo F ya que el criterio nos indica que si dos ángulos son congruentes el tercero también es congruente entre los dos triángulos.
En los siguientes enlaces podrás aprender mucho más sobre la semejanza de triángulos.